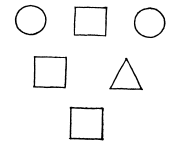
Sudėję duoto triženklio skaičiaus skaitmenis, gavome dviženklį skaičių. Tą patį padarę ir su dviženklio skaičiaus skaitmenimis, gavome vienaženklį skaičių. Visi trys skaičiai gali būti užšifruoti taip, kaip parodyta paveiksle. Koks pradinis skaičius?
Atsakymas: Sakykime, kad skritulį atitinka skaitmuo a, kvadratą — skaitmuo b, o trikampį — skaitmuo c; a, b, c — skirtingi skaitmenys. Kadangi b + c = b , tai c = 0. Tuomet a + b + a = 10b vadinasi, a = 9b/2. Bet b turi būti lyginis, nelygus 0, skaičius ir be to, a = 9/2, b mažiau arba lygu 9. Tuomet a = 9. Vadinasi,
ieškomas skaičius yra 929.


 (-1)
(-1)
[…] http://www.misles.lt/galvosukiai/loginiai-galvosukiai/143-loginiai-galvosukiai/ […]
Tas parašymas, kad a+b+a=10b klaidingas, nes triženklio skaičiaus skaitmenų suma turi būti dviženklis skaičius, o čia “10b” jau triženklis. Mano skaičiavimu maksimalaus triženklio skaičiaus skaitmenų suma gali būti 26 (9+8+9). Kadangi c=0, tada sąlyga lieka a+b+a=bc (arba kitaip a+b+a=b0). Tai reiškia įsitenkant į maksimalų intervalą 26, skaičius kurio antras skaitmuo yra 0 gali būti tik 10 ir 20 (00 negalima). Gaunama a+b+a=10 arba a+b+a=20, o tai a+1+a=10 arba a+2+a=20, a=9/2 arba a=18/2. Kadangi a turi būti sveikas skaičius, todėl a=9, o tai reiškia 929.